文/阿樹 震識:那些你想知道的震識 副總編輯
要寫這篇,真的不容易,要讀這篇,也請讀者有心理準備。本文特別感謝 顏銀桐博士 與 詹忠翰 博士 提供相關研究資訊以及指正。
本文的標題是來自《震識》讀者的問題,可以說是等了幾年,難得一見的好問題,我們終於可以開始談各種更新入的地震風險議題。接下來讓我再細述一下這個問題的始末。
近年來,台灣地震模型(Taiwan Earthquake Model,簡稱「TEM」)結合地質、地震及工程等面向,進行了「台灣機率式地震危害分析(Probabilistic Seismic Hazard Analysis, PSHA) 」的研究,此研究涵蓋了地質、地震及工程等面向。在2015年,TEM公布了包括未來100年、50年與30年台灣可能發生地震的潛勢圖。這是在臺灣第一次有專業人士提供機率式的預估,一開始或許有人會認為這是一種「預測」,不過實際它的用意在於提供較精確的地震風險評估,以應用在都市規畫、耐震設計、災害風險管理以及地震保險等參考。將「明天地震是否會發生」的極大不確定性,用科學、統計與工程的方式盡可能朝問題解決。
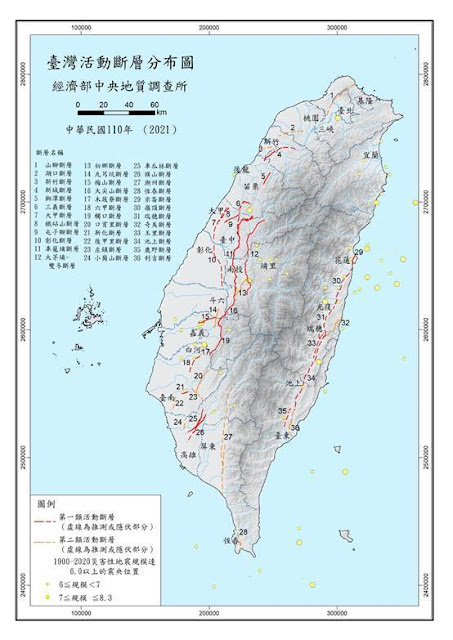
而在2021年,經濟部中央地質調查所(現在整併為經濟部地質調查及礦業管理中心,以下簡稱地礦中心)公告了「水平速度場與斷層活動潛勢圖」,主要是針對地礦中心公告的活動斷層,提供大眾各斷層活動的潛勢。這張圖基本原理一樣是基於前述的PHSA的方式所製作的,只是因為對科學事證與計算細節上的認定有些許差異,而有略為不同的結果。而TEM在2020年也公布了新版的分析結果,有眼尖的「震識」讀者,發現了2020年與2015年的差異,同時也對於評估方式細節有更多好奇,由於阿樹在2021年即撰寫了一系列科普文,因此本文將會是基於這些文章的進階說明。還沒有看過的朋友,或許可以先依序觀看:
而讀者產生的疑惑有兩個:
- 孕震機率最高的是中洲構造,如果再現周期僅100年,那上次地震紀錄在哪呢?怎麼沒有紀錄?
- 彰化斷層的錯動機率為何有時預測很高有時又很低?理論上其上次發生地震在1848年,這樣它的危險性不是比嘉南地區還要高嗎?
這兩個疑惑,我們可以一一拆解。
「再現周期」跟你想的應該不太一樣
再現周期這個詞,聽起來似乎暗示著一種精確的循環,但地震學的研究並非如此。這個概念,其實是建立在長期的地質歷史和統計學上,它告訴我們在過去長達數千甚至數萬年的時間裡,地震發生的大致頻率。舉個例來說,某個斷層在1800年、1910年各發生了一次地震,或許我們可以初步估算它的再現周期是110年,然而它並不代表我們在2020年,或是再往後10年的2030內會看到下一次地震。
為什麼會這樣?那評估地震再現周期到底又有什麼意義咧?首先,斷層活動的「實際周期」確實不會有定值,而在某些斷層甚至有超大的變動。以集集地震的車籠埔斷層為例,最後6次地震之間的發生時距最小約200年,最長約700年,且目前已知最早的2次古地震的時距相距約1,200年,這也代表著地震的能量累積與滑移是個複雜行為。畢竟彈性回跳的過程很長,中間的數十年或數百年間,會影響斷層面上力學性質的因素太多,而板塊活動的能量分配又有許多不同的型式,僅靠實際的地震事件評估,仍會有很大誤差。因此實務上的評估不會僅用歷史地震、地層中古地震事件來評估,還包括推算斷層的滑移速率、區域的構造應力變化或鄰近斷層的交互作用等因素,都會納入再現周期的評估考量。
目前台灣西南部的中洲構造在2020年TEM公告的資料中,發生規模Mw6.9的機率為39%,為目前西半部機率最高的孕震構造。而位於台南的中洲構造,確實過往沒有歷史地震或岩層中的古地震紀錄可以參考,所以科學家會用的方式就是分析斷層崖高度、河階沉積物定年(河階意味著地表受斷層抬升而形成)的資料,推算斷層滑移速率。所以其實「不用有上次地震資料」仍然可以推估再現周期。
確實,這樣的地質推論跟實際有地震紀錄的證據相比,「證據力」不能相提併論,所以實際上在做非直接的再現周期的估算時,還會運用地球物理調查,以及利用統計資料與電腦模擬交叉比對分析。至少跟丟銅板的胡亂猜測比起來,這系列的推論都有一定的科學根據。地球物理調查包括了地表如GPS等大地測量的方式,也算是能直接知道現今斷層的滑移速率,而統計方法則是基於地震是部分隨機的情況,至少我們可以知道這個斷層的大致狀態如何。
最後,在理解了再現周期的概念後,釐清一下中洲構造的資訊。根據TEM整理的結果(陳文山,2010),中洲構造的再現周期為50 ~190年。目前阿樹也沒有查到「再現周期100年」的說法,也許是有人將50 ~190正中間的95當作100?但無論如何,再現周期的計算方式是源自於多項觀測和統計的結果,而統計能告訴我們的並不是「一定」會發生的狀況,而是「機率最大的範圍」,所以一般來說不會直接以一個單一數值呈現,如果有,就會是再次簡化的結果。
 |
| 2015版網頁、2020版網頁 |
BPT模式:
當我們有上一次地震的時間(上圖中To)資料,可先利用它的再現周期可以得到一個機率密度曲線(上圖中紅線),再將現在時間(圖中Tc)和想評估的未來幾年(圖中Tp、A的部分)定出來後,藉由公式就可以得到發生的機率。它考量了過去一次地震的發生時間、斷層性質與彈性回跳理論(密度曲線),所以它是一個兼具統計理論與地震學的評估方式。
 |
| 來源:最具潛勢及歷史災害地震之強地動模擬,國家地震工程中心技術報告(NCREE-2005-032) |
Poisson模式:當沒有足夠的歷史證據時,只能假設這個斷層上的地震為隨機發生,且每個事件都為獨立事件時,一般就會採用這個模式。由於這個假設和彈性回跳理論不符合,所以它可能無法反映真實的風險,而且甚至有低估了地震發生機率的風險可能。
 |
| 來源:潛移行為活動斷層地震潛勢評估方法-以池上斷層為例 |
- 想要估計的時間範圍不同:未來100、50、30年的機率都不同,而理論上時間範圍越大機率會越高,因為地震並非隨機發生的過程。
- 隨著時間有變動:即使什麼都不做、狀態也不變,斷層也沒有發生任何大地震,理論上機率也會越高,因為我們越來越接近下次的大地震了。
- 科學發現或科技進步:地質調查或地球物理觀測資料如果更多、或是有更好的理論模型,都會讓估算有所調整,不過是增是減,就不一定了。
參考資料與延伸閱讀:
台灣地震模型 機率式地震風險評估 (TEM PSHA2020)